[알고리즘] 이분 탐색(Binary Search)
. 등장 배경)
개발하는 데에 있어서 수많은 데이터 중 원하는 값이 어디 있는 지 알아내는 건 매우 중요하다.
그리고 이것을 얼마나 빠르게 알아내는 지는 곧, 우리가 흔히 말하는 최적화와 연관되어 있다.
본 글에서는 편의상 원하는 값을 target, 데이터 리스트를 data_list 라고 표기하겠다.
이분 탐색(Binary Search)가 등장하기 전까지는, 아래 그림과 같은 순차 탐색을 진행했다.
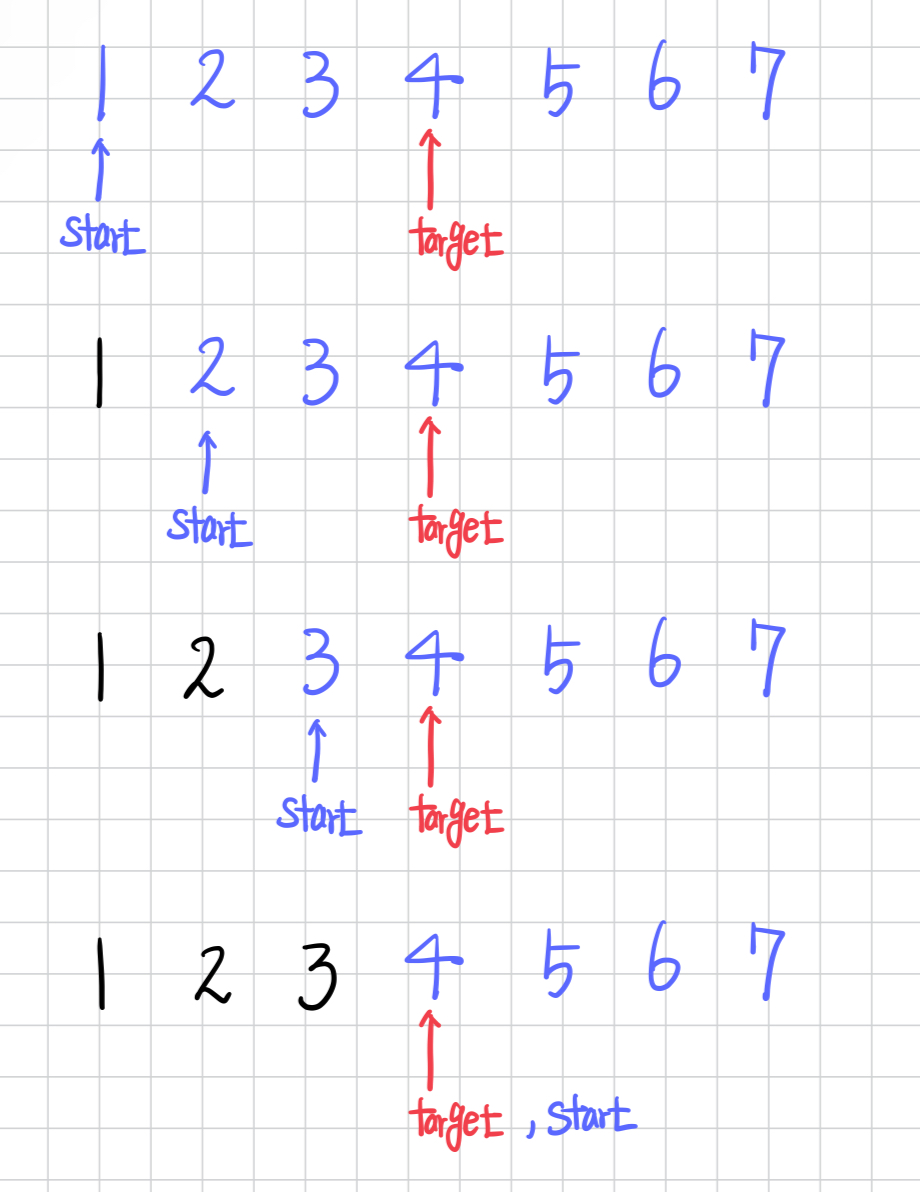
그러나 이와 같은 방식은 data_list를 처음부터 target 값이 나오기까지 하나하나 비교하기에 속도가 매우 느리다.
예를 들어 데이터의 개수 N이 100만개라고 가정한다면, 최악의 경우 100만개의 데이터들을 비교해야 한다.
그렇기에 순차 탐색보다 획기적으로 시행 시간을 단축시킬 수 있는 알고리즘의 사용이 필연적이였다.
. 아이디어)
이분 탐색의 아이디어를 설명하기 전에, 학창 시절 한 번쯤은 겪었을 일화를 예로 들어보고자 한다.
시험을 보고 난 뒤, 친구들에게 내 점수를 말할 때 이렇게 했던 적이 한 번쯤은 있을 것이다.
내 점수 맞춰봐! -> 60점? -> 업(Up). -> 80점? -> 다운(Down). -> 70점? -> 정답!!
이 경우 친구는 본인의 점수를 맞추기까지 3번의 시행 착오를 거쳐 결과를 도출하였다.
그러나 아래 처럼 점수를 맞췄다고 가정해보자.
내 점수 맞춰봐! -> 1점? -> 아니야. -> 2점? -> .... -> 69점? -> 아니야.. -> 70점? -> 정답...!
보기만 해도 아찔하다. 이쯤 되면 70번을 묻고 답한 이들의 인내심이 대단할 정도다.
이 일화를 보고 어느 정도 눈치챘으리라 생각한다.
위는 이분 탐색(Binary Search), 아래는 순차 탐색(Linear Search)의 예시이다.
따라서 이분 탐색의 주 아이디어는 아래와 같다.
1. 만약 내가 제시한 값 X가 target보다 크다면, 범위를 X보다 아래로 설정한다.
2. 만약 내가 제시한 값 X가 target보다 작다면, 범위를 X보다 위로 설정한다.
그리고 실제 알고리즘에서는, 제시한 값 X의 정확성을 높이기 위해 start, end, mid 3가지 변수를 사용한다.
아래는 8개의 데이터 배열을 기준으로 이분 탐색을 진행한 결과를 나타낸 그림이다.

중요한 점은 데이터들이 반드시 정렬되어 있어야 한다는 점이다. 정렬이 되어 있지 않다면 오답을 낼 확률이 매우 높다.
따라서 이분 탐색을 하기 위해서는 빠른 정렬 알고리즘의 동반이 필연적이다.
. 코드)
M1) 재귀 함수로 구현
def Binary_Search(arr,target,start,end): #재귀적 방법
if start>end: #이분 탐색을 끝마쳤는데도 target 값을 못찾았다면
return None #None 을 리턴
mid=(start+end)//2
if arr[mid]==target: #target 값을 찾아냈다면
return mid
elif arr[mid]>target: #target 값보다 크다면
return Binary_Search(arr,target,start,mid-1) #end=mid-1로 변경
else: #target 값보다 작다면
return Binary_Search(arr,target,mid+1,end) #start=mid+1로 변경M2) 반복문으로 구현
def Binary_Search(arr,target,start,end):
while start<=end: #start<=end 인 경우에만 반복하기
mid=(start+end)//2
if arr[mid]==target:
return mid
elif arr[mid]>target:
end=mid-1
else:
start=mid+1
return None #while문을 나왔는데도 return하지 못했다면 target이 없음을 의미. 시간 복잡도)

이분 탐색을 진행할 때마다 평균적으로 리스트 길이가 절반으로 줄어드는 걸 볼 수 있다.
따라서 위 그림과 같이 시행 횟수가 N이 되었을 때 이분 탐색이 끝나므로, 시간 복잡도는 O(log N) 인 걸 알 수 있다.