[알고리즘] KMP 알고리즘

. 등장 배경)

인터넷에서 정보들을 찾아볼 때, 한 번쯤은 Ctrl + F 단축어를 통해 특정 글자만 찾아본 경험이 있을 것이다.
그리고 이 작업은, 대부분의 경우에 아주 빠르게 완료되어 몇 개의 특정 글자가 존재하는 지 알려준다.
KMP 알고리즘은 이러한 작업의 핵심이 되는 알고리즘으로서, 지금도 널리 쓰이고 있는 알고리즘이다.

아래 예시를 통해, KMP 알고리즘의 필요성을 느껴보자.

아이같은아이같은아이작 에서 아이같은아이작 를 찾아보자.
대부분의 경우 아이같은아이.. 에서 멈췄을 것이다.
‘작’이 나와야 할 타이밍에 ‘아’가 나왔기 때문이다.

이렇게 매칭이 실패한 경우 두 번째 글자인 ‘이’부터 탐색을 다시 시작해야 할까?
만약 이렇게 매칭을 하면 정확한 결과는 얻을 수 있다. 브루트포스 알고리즘이기 때문이다.
그러나 만약 문자열의 길이가 1,000,000,000 이라면? 시간이 꽤 많이 소요될 것이다.
상상해 보자. 서칭한 글에서 Ctrl + F 를 눌렀는데 30초 동안 로딩중이라면..?
생각만 해도 아찔하다.

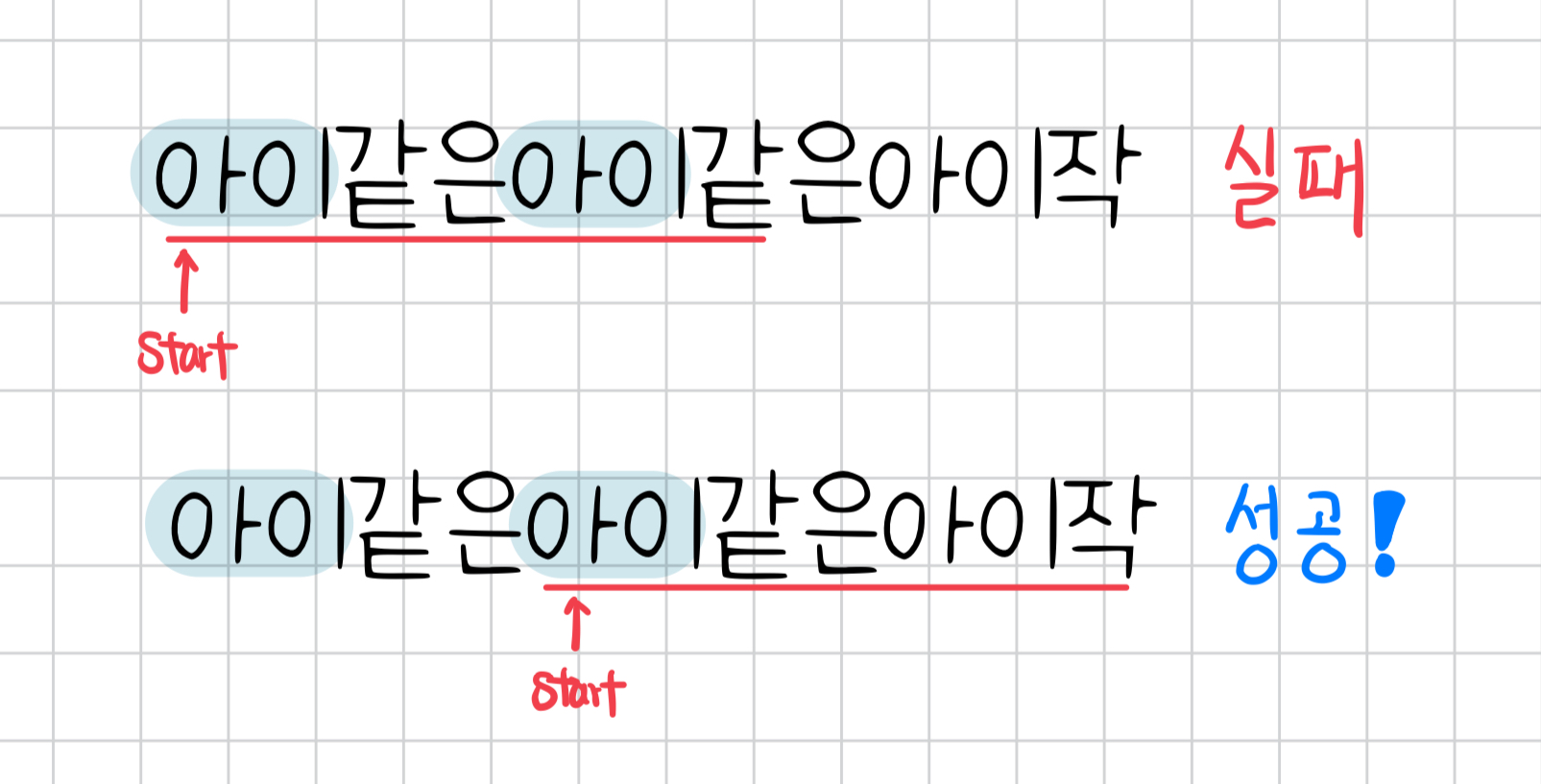
첫 번째 매칭의 사례를 다시 보자. 이 사례는 단순히 매칭에 실패했음만을 알려주고 있지 않다.
어쩌면 가장 중요할 수 있는 정보인, ”아이같은아이“ 까지 매칭이 성공했음을 알려주고 있다.
그리고 이것이 아래에서 설명할 KMP 알고리즘의 핵심 아이디어다.

. 아이디어)

KMP의 구현은 접두사, 접미사의 배열을 저장하는 파이 배열을 만드는 것에서부터 시작한다.
아니 거의 다 매칭한 정보가 아이디어라니, 갑자기 접두사, 접미사라니? 아래 예시를 보자.

기존의 접미사를 새로운 접두사로 인식해 탐색의 속도를 높일 수 있다.

이 처럼, 접두사와 접미사가 같다면, 매칭에 실패했을 때 기존의 접미사를 다시 접두사로 하여금 탐색을 재시작할 수 있다.
재탐색을 시작하는 부분은 기존 매칭에서 실패한 패턴(아이같은아이) 내부(아) 에서시작하기에, 미처 탐색을 하지 못하고 건너뛸 수 있는 것에 대한 걱정 또한 없다.

자 그럼 이제 다음과 같은 의미를 갖는 파이 배열을 만들어보자.
P[i] = 처음부터 i번째 글자까지의 문자열에서, 최대로 겹치는 접두사와 접미사의 길이
이 배열은 초기 인덱스인 i와 1번부터 N-1까지의 인덱스 j를 사용하는데, 아래의 아이디어를 사용한다.

1) pattern[i]과 pattern[j]이 같은 경우
-> i에 1을 더하고, p[j]=i 를 저장한다.

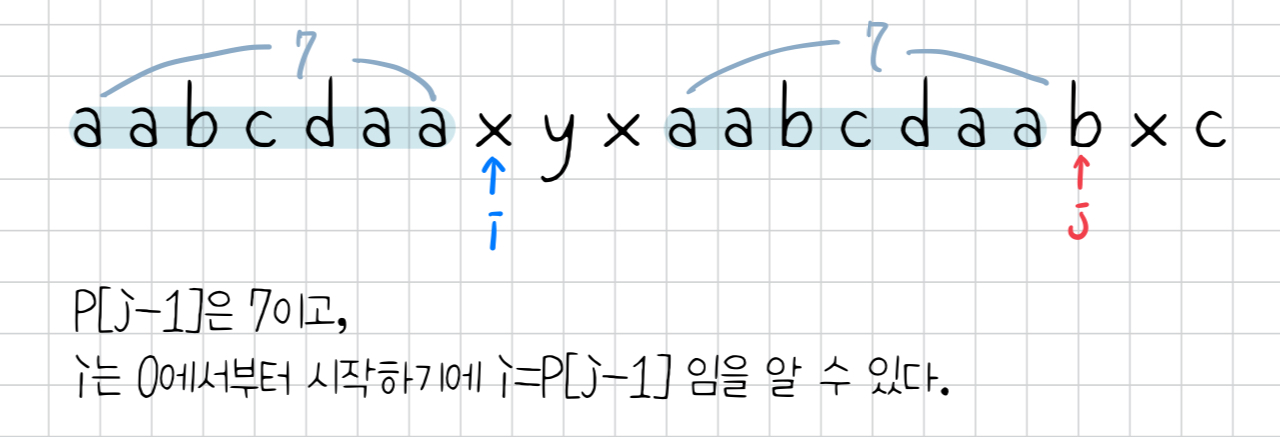
2) pattern[i]과 pattern[j]이 다른 경우
-> i>0이고, pattern[i]==pattern[j]가 될 때까지 i=p[i-1]로 갱신

본 글에서는 초반에 이해가 어려운 2번의 경우에 대해서만 설명을 하겠다.

Step 1

Step 2

Step 3

파이 배열을 만드는 코드는 아래와 같다.

def kmp_table(pattern): 
    p=[0 for _ in range(len(pattern))] #파이 배열 생성
    i=0
    for j in range(1,len(pattern)): #j의 인덱스를 1부터 점차 늘려가면서
        while i>0 and pattern[i]!=pattern[j]: #패턴 끝부분이 일치하지 않는 동안
            i=p[i-1] #i를 p[i-1]로 갱신
        if pattern[i]==pattern[j]: #만약 패턴 끝부분이 일치한다면
            i+=1
            p[j]=i #파이 배열을 갱신
    return p

여기까지 잘 이해했다면 나머지는 바로 이해할 수 있을 거라 생각한다.
실제 문자열에서 패턴을 찾는 알고리즘 또한 위 파이 배열을 만드는 것과 구조가 똑같기 때문이다.

Step 1

Step 2

. 코드)

위에서 설명한 코드와 전체 문자열과 패턴을 비교하는 코드를 합하면 아래와 같다.
res라는 배열을 만든 뒤, 패턴이 일치할 때의 인덱스 값을 넣어주었다.

def kmp(all_string,pattern):
    P=[0 for _ in range(len(pattern))]
    i=0
    for j in range(1,len(pattern)):
        while i>0 and pattern[i]!=pattern[j]:
            i=P[i-1]
        if pattern[i]==pattern[j]:
            i+=1
            P[j]=i
    i=0
    res=[]
    for j in range(len(all_string)):
        while i>0 and all_string[j]!=pattern[i]:
            i=P[i-1]
        if all_string[j]==pattern[i]:
            i+=1
            if i==len(pattern):
                i=P[i-1]
                res.append(j-i+1)
    return res

. 시간복잡도)

전체 문자열의 길이가 N, 패턴의 길이가 M이라면, KMP 알고리즘의 시간 복잡도는 O(N+M)이 된다.
M개의 파이 배열을 구하고, j의 인덱스를 0부터 N까지 이동하면서 비교를 진행하기 때문이다.

이는 기존 문자열 탐색 알고리즘의 시간 복잡도였던 O(N*M)에 비하면 굉장히 획기적인 속도다.
기존 문자열 탐색의 시간 복잡도는 스스로 생각해보길 바란다.

추가로, 필자 역시 KMP 알고리즘을 공부할 때 2일~3일 정도를 필요로 했다.
그만큼 난이도가 있는 알고리즘이고, 처음 봤을 때는 난해하고 이해가 되지 않을 수 있다.
그러나 본 글을 비롯해 많은 글들을 참고하며  꼭 이해하길 바란다.