[백준 #11066번 / Python] 파일 합치기

. 문제)

https://www.acmicpc.net/problem/11032
소설가인 김대전은 여러 파일로 나눠진 소설을 합쳐 최종적으로 하나의 파일로 합치려 한다.
두 개의 파일을 합칠 때 필요한 비용이 두 파일 크기의 합이라 가정한다.
예를 들어 C1,C2,C3,C4가 연속적인 네 개의 장을 수록하고 있는 파일이고, 파일 크기가 40,30,30,50 이라 하자.

첫 번째 방법으론 C2와 C3을 합친 뒤, C1과 합친다. 마지막으로 C4를 합친다.

이 때의 비용은 60+100+150 = 310이다.

 

두 번째 방법으론 C1과 C2를 합치고, C3와 C4를 합친 뒤 두 파일을 서로 합친다.

이 때의 비용은 70+80+150=300이다.

따라서 두 번째 방법이 좀 더 저렴하고, 위처럼 각 파일의 크기가 주어졌을 때 이들을 모두 합치는 최소 비용을 계산하시오.

. 접근)

문제를 잘 읽어보자. 연속된 파일들이 주어져 있고 이들을 잘 더해서 최소의 비용으로 모두 더해야 한다. 그 말은 곧 C1과 C3을 먼저 더한 뒤 C2를 더하는 게 안된다는 뜻이다.

예를 들어 C1~C3 파일을 모두 합친다고 가정하자. 가능한 경우의 수는 아래와 같다.

M1) (C1+C2) + C3 = 70 + 100 = 170

M2) C1 + (C2+C3) = 100 + 60 = 160

 

따라서 i번째 파일부터 j번째 파일까지 합친다고 가정했을 때,

i<k<j인 k에 대하여 sum(Ci~Ck) + sum(Ck+1~Cj)의 최소를 각각의 i와 j마다 구해준다면..?

 

각 경우마다 최솟값을 구할 수 있고, 그 값은 다시 상위의 값을 계산할 때 사용되기 때문에 큰 문제를 각각의 작은 경우로 나눠서 해결할 수 있다는 DP의 성질을 만족한다.

더 나아가, i와 j 사이 간격이 넓을 때 (ex. 파일 C3~C8을 더하는 최솟값) 그 안의 값들에 대해서는 최소 비용이 갱신되어 있는 상태여야 하므로 좁은 간격의 파일들을 더할 때의 최소 비용을 모두 구하고 점점 간격을 넓혀나가는 Bottom-up 방식을 사용해야 할 듯하다.

. 풀이)

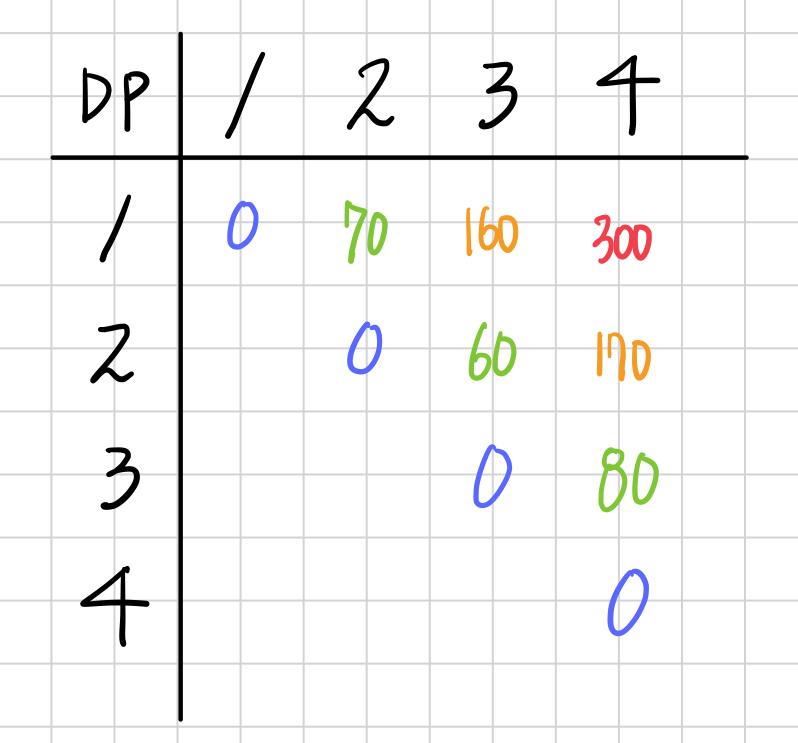
처음 문제에서 제시된 예시를 가지고 DP를 이용해 풀어보자. 이해하기 쉽도록 DP의 Index는 1부터 시작하였다.
접근에서도 나왔듯이, i번째 파일부터 j번째 파일까지 합쳤을 때의 최소 비용을 갱신해나가는 구조이기 때문에,
DP[i][j] = i번째 파일부터 j번째 파일을 합치는 데 필요한 최소 비용 을 의미한다.

먼저, DP[1][1], DP[2][2]와 같은 i=j인 배열에 대해서는 합칠 때 비용이 들어가지 않기에, 0을 넣어준다.

이 후 DP[1][2], DP[2][3]과 같이 간격이 1인 파일들을 합칠 땐 두 파일의 크기만을 더해준다.

이제부터 점화식을 활용할 차례다.

 

아래는 DP[1][3]을 계산하는 두 개의 방법을 나타냈다.

두 방법 중 두 번째 방법이 더 비용이 적게 들기 때문에 DP[1][3]은 min(170,160) = 160이 되고 DP[3][4] 또한 마찬가지다.

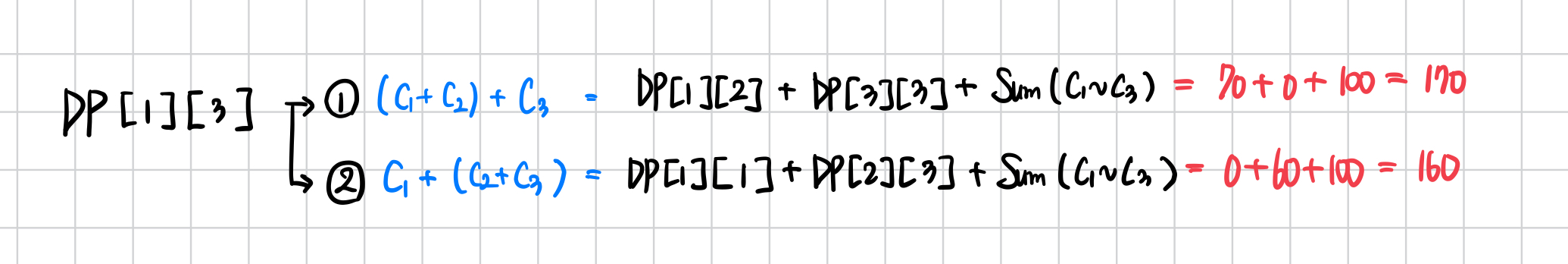
마지막으로, DP[1][4]는 아래와 같은 3가지 방법이 있다.

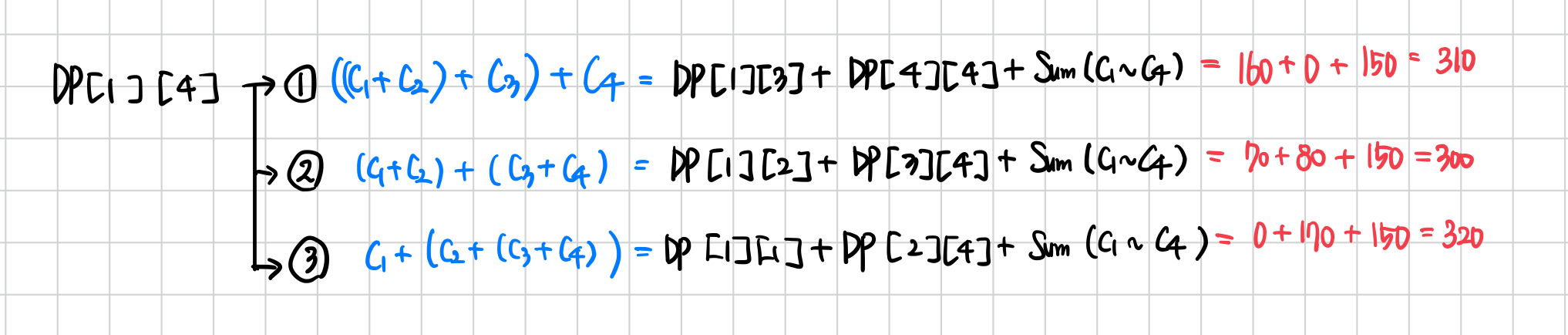
이 중 최솟값은 (C1+C2) + (C3+C4)인 300이므로 DP[1][4] = 300이 되고, 정답을 출력한다.

. 코드)

실제 코드에서는 시간을 줄이기 위해 list의 sum 함수를 사용하기보다는, 부분합을 이용해 O(1)만에 계산할 수 있도록 설계하였다.

import sys, math
input=sys.stdin.readline

Test=int(input())
for _ in range(Test):
    N=int(input())
    file=[0]+list(map(int,input().split()))
    dp=[[math.inf]*(N+1) for _ in range(N+1)]

    subtotal=[0]*(N+1)
    subtotal[0]=0
    for i in range(1,N+1):
        subtotal[i]=file[i]
        subtotal[i]+=subtotal[i-1]

    for x in range(1,N+1):
        dp[x][x]=0
    
    for i in range(2,N+1):
        for j in range(1,N-i+2):
            for k in range(j,j+i-1):
                dp[j][j+i-1]=min(dp[j][j+i-1],dp[j][k]+dp[k+1][j+i-1]+subtotal[j+i-1]-subtotal[j-1])
    
    print(dp[1][N])

. 주의할 점)

실제로 문제를 풀 때, 위 아이디어를 만족하면서 Bottom-up 방식으로 DP를 갱신하는 for문을 짜는 데에 있어서 어려움을 겪었다.
처음 시도에는 대각선마다 갱신하는 것에 아이디어를 얻어 아래와 같은 4중 for문으로 해결했지만, 시간초과 판정을 받았다.

for diagonal in range(1,N+1): #대각선은 1부터 N번까지
    for i in range(1,N-diagonal+2): #i는 1부터 N-diagonal+1까지
        for j in range(diagonal,N+1): #j는 diagonal부터 N까지
            for k in range(i,j): #k는 i부터 j까지
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum(file[i:j+1]))

코드를 뜯어 자세히 생각해보니, 4중 for문은 굉장히 직관적이기에 이해가 쉽다는 장점이 있으나,

똑같은 경우를 반복적으로 계산하는 경향을 보였다.

따라서 처음 봤을 때 조금은 이해가 어렵더라도, 효율적으로 계산하는 for문을 만드는 게 이 문제의 핵심이었다.

문제에서 예시를 든 경우를 자세히 살펴보자. DP를 갱신하는 순서는 아래와 같다.

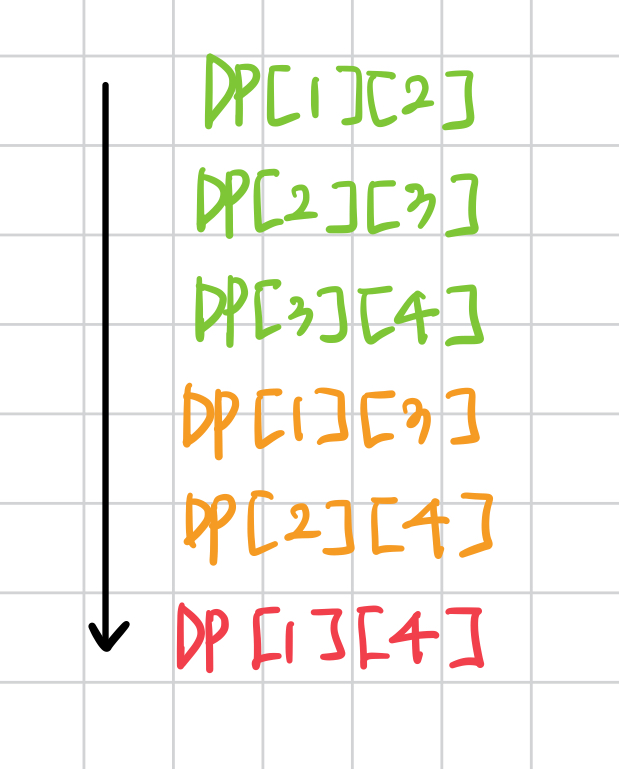
이제 규칙이 보일 것이다. DP[i][j]에서 j는 2,3,4 -> 3,4 -> 4 순으로 진행되고, i는 1,2,3 -> 1,2 -> 1 순으로 진행된다.
따라서 처음 for문에 사용되는 변수는 j, 두 번째 for문은 i, 세 번째 for문은 그렇게 만들어진 i와 j 사이에서 움직이는 k로 지정하여 3중 for문을 만들었다.

for i in range(2,N+1): #i는 2부터 N까지
    for j in range(1,N-i+2): #j는 1부터 N-i+1까지
        for k in range(j,j+i-1): #k는 j부터 j+i까지
            dp[j][j+i-1]=min(dp[j][j+i-1],dp[j][k]+dp[k+1][j+i-1]+subtotal[j+i-1]-subtotal[j-1])

그러나 이 마저도 겨우 pypy3로 풀었는데, 확실히 python이 타 언어에 비해 무겁다는 단점이 이런 곳에서 부각되는 것 같다. (아무튼 풀었으니 만족 ㅎ)